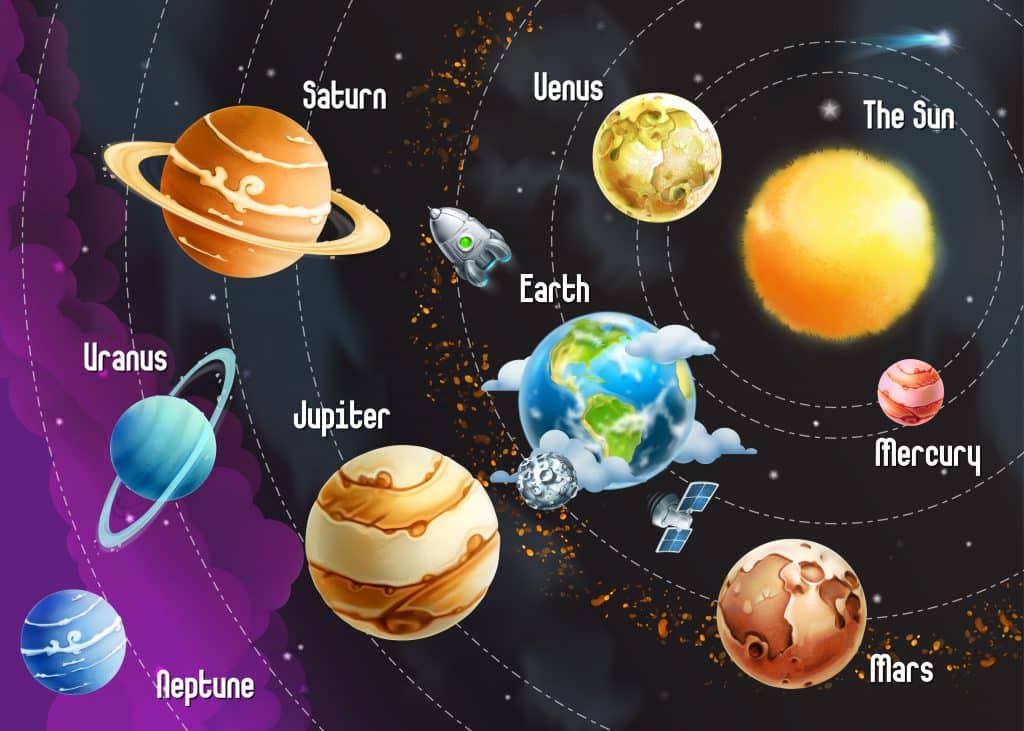
Planets are classified according to their location in the solar system.  Inner planets orbit between the sun and the asteroid belt, and outer planets orbit outside the asteroid belt.  Terrestrial planets are made mainly of rocky material, and giant gaseous planets are primarily made of ice and gas.

Because objects in the solar system are so far apart, astronomers use a larger distance unit than we use on Earth.  On Earth, we often measure distance in meters or kilometers.  Instead, astronomical units (AUs) measure the distance between the objects in the solar system. And 1 AU = 150 million km, the average distance from Earth to the sun.

The inner planets include Mercury, Venus, Earth, and Mars.  Mercury is the planet closest to the sun.  It has no true atmosphere and extreme temperatures.  It is so close to the sun that the side facing the sun during the day reaches temperatures of 430°C.  It has many craters and long, steep cliffs.  Venus is the second planet from the sun and is similar to Earth in size and mass.  It has a highly dense atmosphere of clouds, causing an intense greenhouse effect, which results in temperatures between 450°C and 475°C. Earth is the third planet from the sun.  Here, water exists as a solid, liquid, and gas.  Its atmosphere protects the surface from meteors and the sun’s radiation.  Mars is the fourth planet from the sun.  It’s called the red planet because of the iron oxide present in the rocks on the surface, which gives them their reddish color.  It has a thin atmosphere, which causes extreme temperatures, strong winds, and global dust storms.  It has polar ice caps, seasons, and other evidence that water is or was once present.

The outer planets include Jupiter, Saturn, Uranus, and Neptune.  Jupiter is the largest planet in the solar system and fifth from the sun.  The atmosphere is mainly made up of hydrogen and helium.  Many high-pressure gas storms occur here, with the most notable being the Great Red Spot.  It has at least 60 moons, and four have their own atmosphere.  Saturn is the sixth planet from the sun and the second largest in the solar system.  It has thick outer rings made of hydrogen, helium, ammonia, methane, and water vapor.  Uranus is the seventh planet from the sun, and it is large and gaseous.  The methane in its atmosphere gives the planet a blue-green color.  Its tilted axis of rotation moves around the sun like a rolling ball.  Neptune is the eighth planet from the sun, and it has a frozen surface of nitrogen and geysers that erupt nitrogen gas.

Review:

1. Identify the inner planets.
2. List three characteristics of Mars.
3. List three characteristics of Jupiter.